715キュービットの回路を作り、SATの問題を解くClassiq
This note describes how to use the Classiq platform to solve constraint satisfaction problems, including Kakuro - one problem from our recent Coding Competition. Then, it demonstrates a much more complex example that generates a circuit for 715 qubits.
We Live in a Constrained World
Constraint satisfiability (SAT) problems are everywhere. This difficult class of problems is so far-reaching that there exists an international conference aimed at defining and solving specific cases, with applications such as “Formal Verification, Artificial Intelligence, Operations Research, Computational Biology, Cryptography, Data Mining, Machine Learning, Mathematics, etc.” In every industry, there lies some constraint. Take logistics, for example - applicable to any industry with complex moving parts. The packing of products in a limited volume is just one case of a constraint satisfiability problem, and it’s easy to imagine how fast these problems become impossible to solve. One human can configure a car of luggage, and one team can arrange a closet of supplies, but what’s the best way to optimize the utilization of trans-oceanic shipping containers? Quantum computing offers a quadratic speedup to classical computing when these satisfiability problems are defined and implemented using Grover’s Search Algorithm.
The Kakuro Puzzle
An interesting example of a SAT problem is Kakuro, which was one problem in the Classiq Coding Competition. Kakuro is a logic puzzle similar to Sudoku or a crossword puzzle. The goal is to fill in the empty cells with numbers such that the contents of each row and column add to a specified sum and no two cell numbers in a row or column are the same. For the competition, the problem was to solve the following puzzle using a Grover Search with the fewest CX gates in the oracle after decomposing the circuit into single-qubit unitary gates and CX gates.
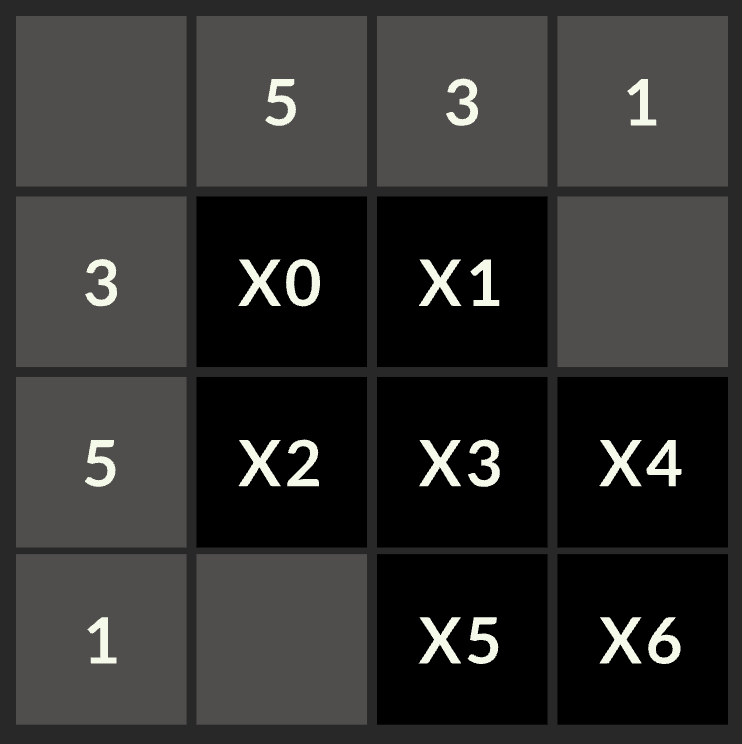
As you start to manually solve this puzzle, it’s clear that the rules of the game can be written in boolean logic for an oracle to solve. X5 and X6 must add to 1, X4 and X6 must add to 1, and so on. After noticing some overlap between the rules, we defined a list of simplified constraints encoding them, with all variables being single-qubit registers except X3, which requires two qubits. A discussion on how these were reduced can be found here. Here are the constraints we must satisfy.
How to solve Kakuro with Classiq
In this note, we'll be solving problems with Classiq's Python SDK, though all results can also be achieved using Classiq's extension in Visual Studio Code. In order to solve this problem using Classiq’s Python SDK, simply define the constraints as an expression within the built-in Arithmetic function. We declare our variables as single-qubit registers, except X3 as a double-qubit register (since it can take the value of 0, 1, 2 or 3), and we adjust our last constraint accordingly.
Now, we specify the hardware settings, declaring our basis gate set of CX and U gates. Lastly, we optimize for CX gate count and synthesize our circuit.
Once we run this code, the Classiq synthesis engine explores - within seconds - various optimization techniques to return a circuit that meets the desired functionality. The returned interactive circuit shown below can be found here, and our resulting depth and CX gate count follows.
To see other solutions created by the competitors over the month-long competition, click here.
Beyond Puzzles
Using the Classiq platform, you can also solve much more sophisticated SAT problems. It’s predicted that quantum computers producing real-world value need hundreds, even thousands of qubits, and Classiq is ready for the massive circuits of the future. Take the following code block in which we synthesize a 715-qubit circuit from a 10 variable, 100 clause oracle.
The 715-qubit interactive circuit generated with this code can be found here.
It’s also not difficult to deploy generated circuits on quantum cloud services. For example, see an in-depth example of executing a SAT problem solved with the Classiq platform on Amazon Braket here.
Ultimately, quantum computers won’t be used just to play logic puzzles or perform simple arithmetic. The advantage offered by quantum computing will be leveraged by any industry with large datasets by searching (solving SAT problems with Grover’s Algorithm), recognizing patterns (quantum machine learning), and optimizing (hybrid classical/quantum QAOA) much faster than ever before. With the low cost of exploring quantum and potentially devastating cost of ignoring it, quantum computing stands to be one of the greatest insurance policies for the future of technology. Whether you’re interested in exploring quantum use cases or you’re ready to take your quantum code to a higher level, the Classiq platform is packed with built-in expertise, allowing you to focus on what problems you’d like to solve, while our synthesis engine focuses on how those problems will be solved.
To learn more about Classiq and our revolutionary software, contact us here, or schedule your no commitment demonstration of the platform here.

This note describes how to use the Classiq platform to solve constraint satisfaction problems, including Kakuro - one problem from our recent Coding Competition. Then, it demonstrates a much more complex example that generates a circuit for 715 qubits.
We Live in a Constrained World
Constraint satisfiability (SAT) problems are everywhere. This difficult class of problems is so far-reaching that there exists an international conference aimed at defining and solving specific cases, with applications such as “Formal Verification, Artificial Intelligence, Operations Research, Computational Biology, Cryptography, Data Mining, Machine Learning, Mathematics, etc.” In every industry, there lies some constraint. Take logistics, for example - applicable to any industry with complex moving parts. The packing of products in a limited volume is just one case of a constraint satisfiability problem, and it’s easy to imagine how fast these problems become impossible to solve. One human can configure a car of luggage, and one team can arrange a closet of supplies, but what’s the best way to optimize the utilization of trans-oceanic shipping containers? Quantum computing offers a quadratic speedup to classical computing when these satisfiability problems are defined and implemented using Grover’s Search Algorithm.
The Kakuro Puzzle
An interesting example of a SAT problem is Kakuro, which was one problem in the Classiq Coding Competition. Kakuro is a logic puzzle similar to Sudoku or a crossword puzzle. The goal is to fill in the empty cells with numbers such that the contents of each row and column add to a specified sum and no two cell numbers in a row or column are the same. For the competition, the problem was to solve the following puzzle using a Grover Search with the fewest CX gates in the oracle after decomposing the circuit into single-qubit unitary gates and CX gates.

As you start to manually solve this puzzle, it’s clear that the rules of the game can be written in boolean logic for an oracle to solve. X5 and X6 must add to 1, X4 and X6 must add to 1, and so on. After noticing some overlap between the rules, we defined a list of simplified constraints encoding them, with all variables being single-qubit registers except X3, which requires two qubits. A discussion on how these were reduced can be found here. Here are the constraints we must satisfy.
How to solve Kakuro with Classiq
In this note, we'll be solving problems with Classiq's Python SDK, though all results can also be achieved using Classiq's extension in Visual Studio Code. In order to solve this problem using Classiq’s Python SDK, simply define the constraints as an expression within the built-in Arithmetic function. We declare our variables as single-qubit registers, except X3 as a double-qubit register (since it can take the value of 0, 1, 2 or 3), and we adjust our last constraint accordingly.
Now, we specify the hardware settings, declaring our basis gate set of CX and U gates. Lastly, we optimize for CX gate count and synthesize our circuit.
Once we run this code, the Classiq synthesis engine explores - within seconds - various optimization techniques to return a circuit that meets the desired functionality. The returned interactive circuit shown below can be found here, and our resulting depth and CX gate count follows.
To see other solutions created by the competitors over the month-long competition, click here.
Beyond Puzzles
Using the Classiq platform, you can also solve much more sophisticated SAT problems. It’s predicted that quantum computers producing real-world value need hundreds, even thousands of qubits, and Classiq is ready for the massive circuits of the future. Take the following code block in which we synthesize a 715-qubit circuit from a 10 variable, 100 clause oracle.
The 715-qubit interactive circuit generated with this code can be found here.
It’s also not difficult to deploy generated circuits on quantum cloud services. For example, see an in-depth example of executing a SAT problem solved with the Classiq platform on Amazon Braket here.
Ultimately, quantum computers won’t be used just to play logic puzzles or perform simple arithmetic. The advantage offered by quantum computing will be leveraged by any industry with large datasets by searching (solving SAT problems with Grover’s Algorithm), recognizing patterns (quantum machine learning), and optimizing (hybrid classical/quantum QAOA) much faster than ever before. With the low cost of exploring quantum and potentially devastating cost of ignoring it, quantum computing stands to be one of the greatest insurance policies for the future of technology. Whether you’re interested in exploring quantum use cases or you’re ready to take your quantum code to a higher level, the Classiq platform is packed with built-in expertise, allowing you to focus on what problems you’d like to solve, while our synthesis engine focuses on how those problems will be solved.
To learn more about Classiq and our revolutionary software, contact us here, or schedule your no commitment demonstration of the platform here.



.svg)











